Data: model 2020
Profil: Matematica-Informatica
Limbaj: C++
Tutoriale Recomandate:
- Cum iei cat mai multe puncte la Bacalaureatul de Informatica
- Functii si parametrii in C++
- Despre recursivitate in informatica
- Componente tare conexe – Algoritmul lui Kosaraju in C++
- Siruri de caractere in C++
- Citirea si scrierea din fisiere text in limbajul C++
- Tipul struct in C++ | Teorie si probleme rezolvate
Subiectul I.
1. Variabilele x, y și z sunt de tip întreg și memorează numere naturale din intervalul [1,103]. Indicați o expresie C/C++ care are valoarea 1 dacă și numai dacă valoarea variabilei x este strict mai mică decât valoarea oricăreia dintre variabilele y și z.
Pentru a rezolva aceasta problema, vom apela la putina matematica.
a. z+x<x+y && x+z>z+y este echivalenta cu z < y && x > y
b. z+x<x+y && z+y>y+x este echivalenta cu z < y && z > x
c. x+z<z+y && z+y>y+x este echivalenta cu x < y && z > x – varianta corecta
d. x+y<y+z && x+z>z+y este echivalenta cu x < z && x > y
2. Subprogramele f1, f2 și f3 sunt definite mai jos. Pentru n=12, se obține aceeași valoare la apelul subprogramelor:
int f1(int n)
{
if(n == 0)
return 1;
return n * f1(n-1);
}
int f2(int n)
{
if(n > 1)
return n * (n - 1) * f2(n-2);
return 1;
}
int f3(int n)
{
int f = 1;
while(n != 0)
{
f = f * n;
n = n - 1;
}
return f;
}
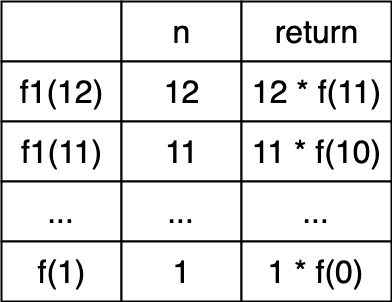
Aici este tabelul pentru f1(n). Daca il analizam, ajungem la concluzia ca aceasta functie returneaza factorialul numarului n transmis ca perametru.
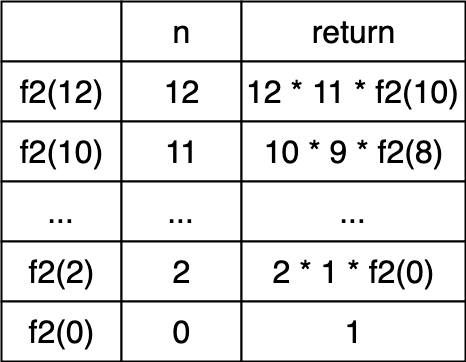
Aici este tabelul pentru f2(n). Il analizam si ajungem la conlcuzia ca si aceasta functie returneaza factorialul numarului n transmis ca parametru.
Aici este tabelul pentru f3(n). Il analizam si ne dam seama ca si aceasta functie returneaza factorialul numarului n transmis ca paremetru.
Asadar, raspunsul corect este d. f1, f2 și f3
3. Având la dispoziție cinci tipuri de prăjituri, cu caise, cu căpșune, cu prune, cu piersici, respectiv cu cireșe, se utilizează metoda backtracking pentru a obține toate posibilitățile de a forma platouri cu câte trei tipuri de prăjituri diferite, știind că în cadrul unui platou nu contează ordinea de așezare a prăjiturilor și că prăjiturile cu căpșune nu vor fi plasate pe același platou cu prăjiturile cu piersici. Primele patru soluții obținute sunt, în această ordine: (caise, căpșune, prune), (caise, căpșune, cireșe), (caise, prune, piersici), (caise, prune, cireșe). A șasea soluție generate este:
Codificam pe rand variantele de raspuns (1 – caise | 2 – capsune | 3 – prune | 4 – piersici | 5 – cirese), si de asemenea trebuie sa fim atenti deoarece 2 (capsunele) si 4 (piersicile) nu trebuie sa se regaseasca in nici o combinatie. Generam urmatoarele doua variante si decodificam raspunsul la final.
Raspunsul corect este: c. (căpșune, prune, cireșe)
4. Un arbore cu 8 noduri, numerotate de la 1 la 8, are drept rădăcină nodul numerotat cu 5 și muchiile [1,5], [2,7], [3,7], [3,6], [4,5], [5,7], [7,8]. Indicați numărul de noduri care sunt descendenți direcți („fii”) ai nodului 7.
Desenam arborele si numaram cate noduri avem.
Avem nodurile 2, 3 si 8. Deci varianta corecta de raspuns este
5. Un graf orientat are 10 arce, 3 componente tare conexe, iar fiecare vârf al său are atât gradul interior, cât și gradul exterior nenule. Numărul minim de noduri pe care le poate avea graful este:
Pe aceasta problema nu sunt 100% sigur de desen. Am presupus ca avem 3 componente conexe:
- Componenta 1: Nodurile 1 si 2
- Componenta 2: Nodurile 3 si 4
- Componenta 3: Nodurile 4 si 5
Raspunsul corect este: b) 5
Subiectul II.
1. Algoritmul alăturat este reprezentat în pseudocod. S-a notat cu a%b restul împărțirii numărului natural a la numărul natural nenul b.
citește m,n,x (numere naturale nenule, m ≤ n)
s <- 0; pm <- 1; pn <- 1
repetă
dacă m % x = 0 atunci
s <- s + m; pm <- x
dacă n % x = 0 şi m ≠ n atunci
s <- s + n; pn <- x
m <- m + pm
n <- n - pn
până când m > n
scrie s
a) Scrieți valoarea afișată în urma executării algoritmului dacă se citesc, în această ordine, numerele 21, 38 și 4.
Facem un tabel pentru a urmarii mai usor cum se modifica valorile.
Asadar, raspunsul corect este: 120.
b) Dacă pentru m şi x se citesc numerele 20, respectiv 2020, scrieți cea mai mică şi cea mai mare valoare care pot fi citite pentru variabila n, astfel încât, pentru fiecare dintre acestea, în urma executării algoritmului, să se afişeze 2020.
Observam faptul ca numerele m si n, dupa ce sunt adunate la s, urmeaza sa scada cu exact valoarea lui x. Asa ca ne oferim de acest aspect si vedem faptul ca cel mai mic numar ce n poate sa il aiba este 2020.
Observam faptul ca pentru n = 4040, dupa adunare s va fi 4040, asa ca ne gandim la un numar mai mic. Urmatorul numar este n = 4039, la “s” adunandu-se 2020 (datorita lui m).
c) Scrieți programul C/C++ corespunzător algoritmului dat.
#include <iostream>
using namespace std;
int main()
{
int s, pm, pn;
unsigned int m, n, x;
cin >> m >> n >> x;
s = 0, pm = 1, pn = 1;
do
{
if(m % x == 0)
{
s = s + m;
pm = x;
}
if(n % x == 0 && m != n)
{
s = s + n;
pn = x;
}
m = m + pm;
n = n - pn;
} while(m <= n);
cout << s;
return 0;
}
d) Scrieți în pseudocod un algoritm, echivalent cu cel dat, înlocuind structura repetă…până când cu o structură de alt tip.
citește m,n,x (numere naturale nenule, m ≤ n)
s <- 0; pm <- 1; pn <- 1
cat timp m <= n executa
dacă m % x = 0 atunci
s <- s + m; pm <- x
dacă n % x = 0 şi m ≠ n atunci
s <- s + n; pn <- x
m <- m + pm
n <- n - pn
scrie s
2. Variabila p memorează, pentru fiecare dintre cele 20 de zone de parcare ale unui oraș, următoarele date specifice: identificatorul zonei, numărul de locuri închiriate pe parcursul lunii curente, precum și prețul practicat în zona respectivă pentru închirierea unui loc pentru o lună. Știind că expresiile C/C++ de mai jos au ca valori câte un număr natural, reprezentând identificatorul primei zone, respectiv suma obținută în urma închirierii pe parcursul lunii curente a tuturor locurilor de parcare din această zonă, scrieți definiția unei structuri cu eticheta parcare, care să permită memorarea datelor specifice unei zone de parcare, și declarați corespunzător variabila p.
p[0].id p[0].numar*p[0].pret
struct parcare{
int id;
int numar;
int pret;
}p[20];
3. Variabila i este de tip întreg, iar variabila a memorează un tablou bidimensional cu 5 linii și 7 coloane, numerotate începând cu 0, cu elemente numere întregi. Fără a utiliza alte variabile decât cele menționate, scrieți o secvență de instrucțiuni în urma executării căreia să se afișeze pe ecran, separate prin câte un spațiu, indicii liniilor cu proprietatea că primul sau ultimul lor element are valoarea 2020.
for(int i = 0; i <= 5; i++)
{
if(a[i][0] == 2020 || a[i][6] == 2020)
cout << i << " ";
}
Subiectul III.
1. Subprogramul duplicare are doi parametri:
- n, prin care primește un număr natural (n∈[1,104]);
- d, prin care furnizează numărul obținut prin duplicarea fiecărei cifre impare a lui n sau -1 dacă acesta nu are nicio cifră impară.
Scrieți definiția completă a subprogramului.
Exemplu: dacă n=2019, după apel d=201199
void duplicare(int n, int &d)
{
int invers = 0;
int ok = 0;
while(n != 0)
{
int c = n % 10;
invers = invers * 10 + c;
if(c % 2 != 0)
{
invers = invers* 10 + c;
ok = 1;
}
n = n / 10;
}
if(ok == 1)
{
d = 0;
while(invers != 0)
{
int c = invers % 10;
d = d * 10 + c;
invers = invers / 10;
}
}
else
d = -1;
}
2. Un text are cel mult 100 de caractere, iar cuvintele sale sunt formate numai din litere mici ale alfabetului englez și sunt separate prin câte un spațiu. Scrieți un program C/C++ care citește de la tastatură un număr natural n (n∈[1,102]), apoi un text de tipul precizat mai sus, și afișează pe ecran cuvintele acestuia, pe rânduri separate, astfel încât primele poziții să fie ocupate de mulțimea formată de cele care au cel puțin n litere, iar următoarele poziții, în continuarea acestora, să fie ocupate de mulțimea celorlalte cuvinte. Cuvintele din aceeași mulțime sunt afișate într-o ordine oarecare, iar dacă una dintre cele două mulțimi este vidă, se afișează pe ecran doar mesajul nu exista.
Exemplu: pentru n=5 și textul el mergea tot spre aleea pietruita
datele afișate pot fi cele alăturate.
mergea | aleea | pietruita | el | tot | spre
#include <iostream>
#include <cstring>
using namespace std;
int main()
{
char s[101];
char s1[101] = "", s2[101] = "";
unsigned int n;
unsigned int totalCuvinte = 0, totalCuvinteGn = 0, totalCuvinteLn = 0;
cin >> n;
cin.get();
cin.getline(s, 100);
char *cuvant = strtok(s, " ");
while(cuvant != NULL)
{
if(strlen(cuvant) >= n)
{
strcat(s1, cuvant);
strcat(s1, " ");
totalCuvinteGn++;
}
else
{
strcat(s2, cuvant);
strcat(s2, " ");
totalCuvinteLn++;
}
totalCuvinte++;
cuvant = strtok(NULL, " ");
}
if(totalCuvinteGn != 0 && totalCuvinteLn != 0)
{
cuvant = strtok(s1, " ");
while(cuvant != NULL)
{
cout << cuvant << "\n";
cuvant = strtok(NULL, " ");
}
cuvant = strtok(s2, " ");
while(cuvant != NULL)
{
cout << cuvant << "\n";
cuvant = strtok(NULL, " ");
}
}
else
{
cout << "nu exista";
}
return 0;
}
3. Fișierul numere.in conține pe prima linie un număr natural n (n∈[2,109]), iar pe a doua linie un șir de cel mult 109 numere naturale din intervalul [1,n]. Numerele din șir sunt ordonate descrescător și sunt separate prin câte un spațiu. Se cere să se determine numărul valorilor naturale distincte din intervalul [1,n] care NU se găsesc în șirul menționat mai sus. Numărul determinat se afișează pe ecran. Proiectați un algoritm eficient din punctul de vedere al spațiului de memorie și al timpului de executare.
Exemplu: dacă fișierul conține numerele
10
8 8 8 5 3 3
se afișează pe ecran 7 (în șir nu se găsesc valorile 10 9 7 6 4 2 1).
a) Descrieți în limbaj natural algoritmul proiectat, justificând eficiența acestuia.
Algoritmul meu numara pe rand cate numere lipsesc, retinand tot timpul ultimele doua valori citite. Citim mai intai n, iar mai apoi primul numar din sir. Calculam cat este diferenta intre n si x, si o adaugam in variabila “total”. Algoritmul continua sa adauge diferenta intre ultimele doua numere citite pana cand ajunge la ultimul numar. Odata ce a ajuns la ultimul numar parcurge “nr”, adauga diferenta lipsa dintre “nr” si 1.
Algoritmul este eficient din punct de vedere al memoriei, deoarece nu retinem nicaieri toate numerele citite. De asemea, algoritmul este eficient si din punct de vedere al timpului, avand o complexitate liniara O(N) – unde N este numarul total de elemente din fisier.
b) Scrieți programul C/C++ corespunzător algoritmului proiectat
#include <iostream>
#include <fstream>
using namespace std;
ifstream fin("numere.in");
int main()
{
unsigned int total = 0;
unsigned int n;
unsigned int x, y;
fin >> n;
fin >> x;
y = x;
total = total + (n - x);
while(fin >> x)
{
if(x != y)
total = total + (y - x - 1);
y = x;
}
total = total + (x - 1);
if(total != 0)
cout << total;
else
cout << "NU";
return 0;
}
