Vectori de frecventa / aparitii – Tablouri unidimensionale

Vector de frecventa (aparitii) – Ce este?

Vectorul de frecvente reţine numărul de apariţii al fiecărei valori citite într-un vector. Folosirea vectorului de frecvenţe permite scrierea unor algoritmi eficienţi în cazul în care datele de intrare au valori dintr-un domeniu cunoscut care poate fi prelucrat rapid.

Utilizarea unui vector de frecventa este oportuna cand trebuie sortate (crescator/descrescator) valori, sau prelucrate informatii din domenii inguste (litere, numere de cateva cifre, etc). In general se pot folosii vectorii de frecventa daca numarul total al elementelor posibile nu depaseste 1 milion.

Observatie: In unele carti de specialitate (manuale) mai apare notiunea de vector caracteristic. Este un vector de frecvente care memoreaza doar 0 sau 1 (elementul apare, sau nu, in citire).

Ce aplicatii au in viata reala vectorii de frecventa?

Gandeste-te la urmatorul scenariu: esti cu prietenii tai la Laser Tag (un joc in care va impuscati intre voi cu lasere) si doriti sa stabiliti cine este cel mai bun jucator dintre voi. Pentru a calcula acest “skill” ajungeti la concluzia ca ar fi excelent daca ati tine cont:

• cati jucatori a impuscat fiecare (kills)
• de cate ori a fost impuscat fiecare jucator (deaths)

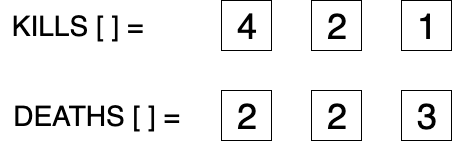
In imaginea de mai sus am luat 3 jucatori:

• Jucatorul 0 (Catalin)
• Jucatorul 1 (Cristi)
• Jucatorul 2 (Mihai)

Si am stabilit urmatorul scenariu:

• Catalin impusca de 4 ori (de 2 ori pe Mihai si de doua ori pe Cristi) si este impuscat de 2 ori (o data de Mihai si o data de Cristi)
• Cristi impusca de 2 ori (o data pe Mihai si o data pe Catalin) si este impuscat de 2 ori.
• Mihai impusca o data si este impuscat de 3 ori.

Putem sa contorizam aceste scoruri folosind doi vectori de aparitii.

• Primul vector se va numii Kills, unde Kills[i] semnifica de cate ori a impuscat jucatorul cu numarul i pe cineva.
• Al doilea vector se va numii Deaths, unde Deaths[i] semnifica de cate ori a fost impuscat jucatorul cu numarul i.

Vectorii de frecventa (aparitii) – Problema aplicata

In fisierul exemplu.in citeste un numar n, dupa care n cifre (unde n poate fi cel mult 10,000,000). Sa se afiseze fiecare cifra care apare precum si numarul ei de aparitii.

Deoarece avem 10 milioane de numere ce se pot regasii in fisier, este evident faptul ca nu le vom stoca niciunde, deoarece am ocupa foarte multa memorie.

In schimb ne bazam pe urmatoarea observatie: deoarece numerele ce se pot regasii in vectorul nostru X sunt foarte limitate (adica putem gasii doar cifre de la 0 – 9) – putem creea un alt vector “V[10]”, V[i] semnificand de cate ori apare cifra “i” in vectorul nostru initial “X”.

#include    <iostream>
#include    <fstream>

using namespace std;

ifstream fin("exemplu.in");

int V_FR[10]; // Vector de frecventa
int V_CA[10]; // Vector caracteristic
int main()
{
    int n;
    fin >> n;
    for(int i = 1; i <= n; i++)
    {
        int nr;
        fin >> nr; // Citesc toate numerele din fisier

        V_FR[nr]++; // Incrementez pozitia nr citit in vectorul V_FR

        if(V_CA[nr] == 0)
            V_CA[nr] = 1;
    }

    // Vectorul caracteristic
    cout << "In fisier apar urmatoarele cifre: ";
    for(int i = 0; i <= 9; i++)
    {
        if(V_CA[i] != 0)
            cout << i << " ";
    }

    // Vectorul de aparitii
    cout << "\n\nIn fisier apar urmatoarele cifre: \n";
    for(int i = 0; i <= 9; i++)
    {
        if(V_FR[i] != 0)
            cout << i << " apare de " << V_FR[i] << " ori\n";
    }
    return 0;
}

Probleme rezolvate:

1. Se da un sir cu cel putin 3 si cel mult 1.000.000.000 de numere naturale din intervalul [0, 1.000.000]. Se cere sa se afiseze pe ecran, separate printr-un spatiu, doua numere distincte, anume cel mai mare numar impar cu doua cifre si cel mai mic numar par cu doua cifre care NU fac parte din sir. Daca nu exista doua astfel de valori se va afisa pe ecran mesajul nu exista.

Observam mai multe aspecte in aceasta problema:

• Putem avea in total 1 miliard de numere, ceea ce este enorm. Asta ne indica faptul ca nu ar trebuii sa salvam niciunde aceste numere
• Posibilele numere se afla in intervalul [0, 1.000.000]
• Trebuie sa obtinem o informatie despre numerele cu doua cifre -> acest aspect ne indica faptul ca putem folosii un vector de aparitii pentru numerele din intervalul [10, 99]

#include    <iostream>
#include    <fstream>

using namespace std;

ifstream fin("exemplu.in");

int AP[100];
int main()
{
    int n;
    fin >> n;
    for(int i = 1; i <= n; i++)
    {
        int nr;
        fin >> nr; // Citesc toate numerele din fisier
        if(nr >= 10 && nr <= 99)
            AP[nr]++;
    }

    int nrMare, nrMic, gasit = 0;
    for(int i = 99; i > 10; i = i - 2)
    {
        if(AP[i] == 0)
        {
            nrMare = i ;
            gasit++;
            break;
        }
    }

    for(int i = 10; i < 99; i = i + 2)
    {
        if(AP[i] == 0)
        {
            nrMic = i;
            gasit++;
            break;
        }
    }

    if(gasit == 2)
        cout << nrMic << " " << nrMare;
    else
        cout << "nu exista";

    return 0;
}

2. Fişierul bac.txt conţine un şir de cel puțin două și cel mult 10⁶ numere naturale din intervalul [0,10³], separate prin câte un spaţiu. Șirul are cel puțin un termen par și cel puțin un termen impar. Se cere să se afișeze pe ecran termenii șirului, separați prin câte un spaţiu, astfel încât toți cei impari să apară înaintea tuturor celor pari, şi atât subșirul format din cei impari, cât şi subșirul format din cei pari, să fie în ordine crescătoare, ca în exemplu. Proiectați un algoritm eficient din punctul de vedere al timpului de executare.
Exemplu: dacă fişierul conţine numerele 4 2 3 1 2 5 se afişează pe ecran: 1 3 5 2 2 4

Pe masura ce citim numerele, incrementam pozitia lor corespunzatoare paritatii numarului. In acelasi timp memoram cel mai mare nr impar si cel mai mare nr par citit. La final parcurgem vectorii de aparitii pana la maximul lor corespunzator si afisam numerele in ordine crescatoare.

Acest algoritm este eficient din punct de vedere al spatiului, deoarece nu trebuie sa memoram 100,000 numere. De asemenea, nu mai este nevoie de nici o sortare ulterioara, deoarece folosind vectorii de aparitie, avem garantat faptul ca numerele vor aparea in ordine crescatoare. Complexitatea acestui algoritm este liniara in O(n) – unde n este numarul total de numere din fisier.

#include    <iostream>
#include    <fstream>

using namespace std;

ifstream fin("bac.txt");

int impare[1001];
int pare[1001];

int main()
{
    int n;
    int maxImp = -1, maxPar = -1;
    while(fin >> n)
    {
        if(n % 2 == 0)
        {
            if(n > maxPar)
                maxPar = n;
            pare[n]++;
        }
        else
        {
            if(n > maxImp)
                maxImp = n;
            impare[n]++;
        }
    }

    for(int i = 1; i <= maxImp; i++)
    {
        for(int ap = 1; ap <= impare[i]; ap++)
            cout << i << " ";
    }
    
    for(int i = 0; i <= maxPar; i++)
    {
        for(int ap = 1; ap <= pare[i]; ap++)
            cout << i << " ";
    }
    return 0;
}