Ridicarea la putere in C++

Cum am calcula in mod normal N^P ? Cea mai usoara metoda este sa facem:

#include    <iostream>

using namespace std;

int main()
{
    int N, P;
    long long result = 1;
    cin >> N >> P;

    for(int i = 1; i <= P; i++)
        result = result * N;

    cout << result;

    return 0;
}

Sau folosind libraria #include <math>:

#include    <iostream>
#include    <cmath>

using namespace std;

int main()
{
    int N, P;
    cin >> N >> P;
    cout << pow(N, P);

    return 0;
}

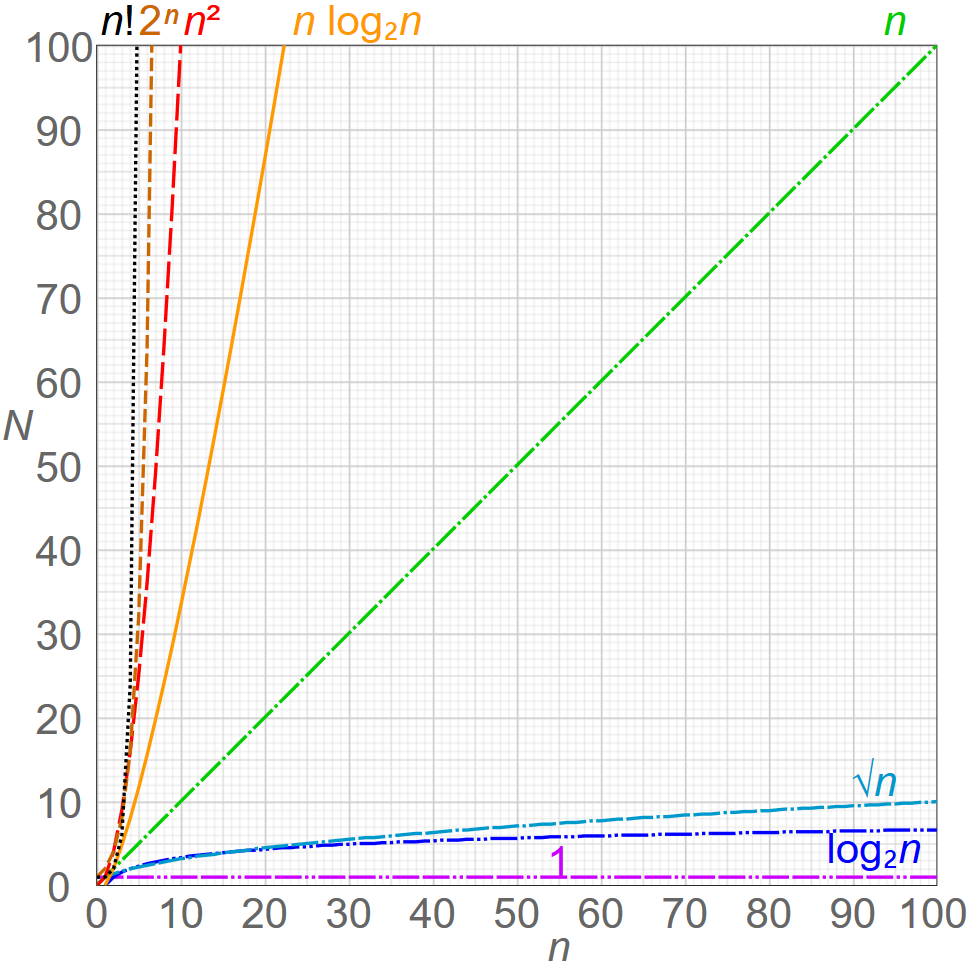
Insa aceste metode sunt foarte ineficiente. Deoarece daca N si P sunt numere naturale, putem aplica un algoritm mai inteligent si reducem complexitatea in timp de la O(P) (unde P este exponentul) la O(log₂(P)). Diferenta intre aceste doua complexitati poate fi vazuta in graficul de mai jos:

Graficul complexitatii in timp

Ridicarea la putere in timp logaritmic

Tot algoritmul se bazeaza pe urmatoarea observatie:

Observatie ridicarea la putere in timp logaritmic

Aceasta metoda foloseste reprezentarea pe biti a numerelor pentru a determina ce calcule trebuie efectuate.

In urmatorul exemplu o sa va  aratam cum putem calcula x¹³ folosind aceasta metoda. Exponentul, 13, este scris sub forma 1 1 0 1 in codul binar. De asemenea, inca un aspect important este faptul ca bitii sunt folositi de la stanga la dreapta. De asemenea, 13 folosind doar 4 biti in reprezentarea lui, se vor efectua doar 4 iteratii.

De asemenea 13 poate fi scris sub forma 13 = 2³ + 2² + o + 2⁰.

In primul rand ne luam o variabila “rezultat” pe care o vom initializa r= 1 (1 = x⁰).

Calculam:

• r = r * r . Deoarece primul bit este 1 (impar), mai adaugam un “x” la rezultat. Si avem r =  r * x. Deci avem r = 1 * x, adica x¹
• r = r * r. Inlocuind, x¹ * x¹ = x² Deci r= x². Deoarece al doilea bit este 1 (impar), mai adaugam un “x” la rezultat si avem. r = x² * x, adica x³
  
• r = r * r. Inlocuind, x³ * x³ = x^6. Deci r = x⁶. Deorece al treilea bit este o, nu mai adaugam nimic.
• r = r * r. Inlocuind, x⁶ * x⁶ = x¹². Deci r = x¹². Deoarece al patrulea bit este 1 (impar), mai adaugam un “x” la rezultat si obtinem r = x¹² * x, adica x¹³.

De unde rezulta complexitatea in timp log₂(P)?

In mod normal pentru a calcula N^P am calcula N = N * P de P ori. Ceea ce ar rezulta intr-o complexitate O(P).

Dar daca folosim metoda descrisa mai sus o sa utilizam log₂(P) operatii. Mai pe scurt numarul de pasi depinde de numarul de biti ce il ocupa P in memorie.
Am vazut mai sus ca pentru 13 am folosit log₂(13) = 4 operatii.

Problema lgput – infoarena.ro

In continuare, pentru implementarea algoritmului vom rezolva problema lgput de pe infoarena.ro.

Cerinta:

Dandu-se doua numere naturale N si P, se cere sa se calculeze restul impartirii lui N^P la 1999999973.

De ce trebuie sa calculam impreuna cu restul impartirii la 1999999973? Deoarece daca am calcula in mod normal 2³² ridicat la puterea 2³² ar trebuii sa modificam putin mai mult algoritmul datorita afisarii. Si nu acesta este scopul problemei.

Varianta nerecursiva:

/* Tutoriale-Pe.NET - Ridicarea la putere in timp logaritmic
 * Link: https://tutoriale-pe.net/ridicarea-la-putere-timp-logaritmic-c/
 * Rezolvare infoarena: http://www.infoarena.ro/problema/lgput
 */
#include    <iostream>
#include    <fstream>

using namespace std;

ifstream fin("lgput.in");
ofstream fout("lgput.out");

const int MOD = 1999999973;

int RidicareLogaritmica(int N, int P)
{
    int r = 1;
    while(P)
    {
        if(P % 2 == 1)
            r = (1LL * r * N) % MOD;
        N = (1LL * N * N) % MOD;
        P = P / 2;
    }
    return r;
}

void Read()
{
    int N, P;
    fin >> N >> P;
    fout << RidicareLogaritmica(N, P);
}

int main()
{
    Read();
    return 0;
}