Data: simulare 2020 (varianta 1)
Profil: Matematica-Informatica
Limbaj: C++
Tutoriale Recomandate:
- Cum iei cat mai multe puncte la Bacalaureatul de Informatica
- Functii si parametrii in C++
- Despre recursivitate in informatica
- Siruri de caractere in C++
- Citirea si scrierea din fisiere text in limbajul C++
- Tipul struct in C++ | Teorie si probleme rezolvate
Subiectul I.
1. Indicați o expresie C/C++ care are valoarea 1 dacă şi numai dacă numărul natural memorat în variabila întreagă n este divizibil cu 2 şi cu 5.
a. !(n%2==1 || n%5!=0) este echivalent cu (n % 2 != 1 && n % 5 == 0) – varianta corecta
b. !(n/2==1 && n/5!=0) este echivalent cu (n / 2 != 1 || n / 5 == 0)
c. n%2==0 || !(n%5==0) este echivalent cu (n % 2 == 0 || n % 5 != 0)
d. n/2==0 && !(n/5==0) este echivalent cu (n / 2 == 0 && n / 5 != 0)
2. Subprogramul f este definit alaturat. Indicați valoarea f(102030).
int f(int x)
{
if(x > 20)
return 20 + f(x / 10);
return 2020;
}
Rezultatul final va fi: 2020 + 20 + 20 + 20 + 20 = 2100 (varianta c)
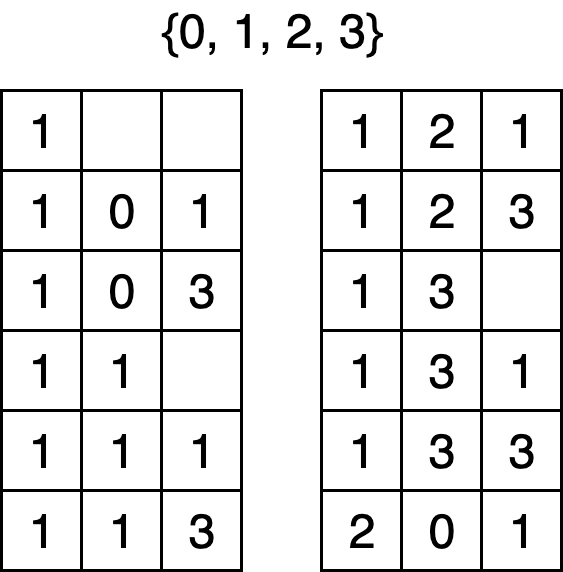
3. Utilizând metoda backtracking, se generează toate numerele impare de cel mult trei cifre din mulţimea {0, 1, 2, 3}. Primele 8 soluţii generate sunt, în această ordine: 1, 101, 103, 11, 111, 113, 121, 123. Cea de a 12-a soluţie generată este:
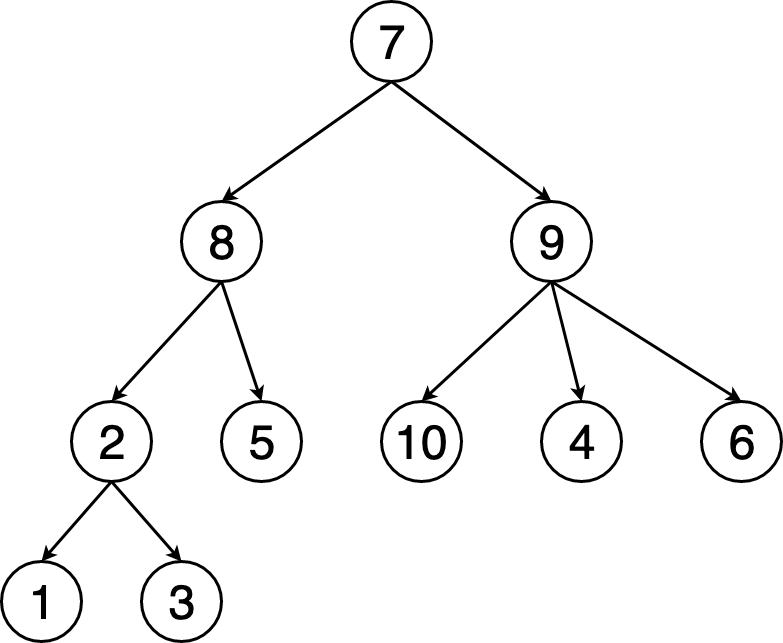
4. Un arbore cu 10 noduri, numerotate de la 1 la 10, este reprezentat prin vectorul de „taţi” (2,8,2,9,8,9,0,7,7,9). Indicați câte dintre nodurile arborelui au exact doi fii.
Nodurile 2, 8 si 7 au exact doi fii, deci raspunsul este b. 3
5. Un graf neorientat cu 20 de noduri are 100 de muchii. Numărul de muchii ce trebuie adăugate, pentru ca graful obţinut să fie complet, este:
Un graf complet presupune ca avem legatura directa intre oricare doua noduri. Aplicam formula pentru graf complet – numarul de muchii: (n * (n – 1)) / 2 = 190 muchii. Drept urmare, trebuie sa adaugam 90 de muchii. Drept urmare este varianta c).
Subiectul II.
1. S-a notat cu a%b restul împărţirii numărului natural a la numărul natural nenul b şi cu [c] partea întreagă a numărului real c.
citeşte n(număr natural) p <- 1; m <- 0; k <- 0 cât timp n≠0 execută --- citește x (număr natural) --- pentru i <- 1,k execută ------ x <- [x/10] --- dacă x≠0 atunci c <- x%10 ------ altfel c <- n%10 --- m <- c * p + m --- n <- [n/10] --- p <- p*10; k <- k+1 scrie m
a) Scrieţi valoarea care se afişează în urma executării algoritmului dacă se citesc, în această ordine, numerele 12345, 780, 921, 4013, 75, 100214.
b) Dacă pentru n se citește numărul 49, scrieți două seturi de date care pot fi citite în continuare astfel încât, pentru fiecare dintre acestea, în urma executării algoritmului, să se afișeze 49.
Facem urmatoarea observatie – cum am format numarul 2020? Am luat pe rand fiecare cifra din x: mai intai am luat prima cifra din primul numar (0 din 780), mai apoi am luat cifra zecilor din al doilea numar (2 din 921), pe urma am luat cifra sutelor din al treilea numar (0 din 4013). Asadar cum se formeaza numarul? Pentru a putea obtine 49 trebuie sa luam doua numere astfel incat:
- In primul numar pe cifra unitatilor (prima cifra din dreapta) sa fie 9
- In al doilea numar pe cifra zecilor (a doua cifra din dreapta) sa fie 4
c) Scrieţi programul C/C++ corespunzător algoritmului dat.
#include <iostream>
using namespace std;
int main()
{
unsigned int n, p = 1, m = 0, k = 0, x, c;
cin >> n;
while(n != 0)
{
cin >> x;
for(int i = 1; i <= k; i++)
x = x / 10;
if(x != 0)
c = x % 10;
else
c = n % 10;
m = c * p + m;
n = n / 10;
p = p * 10;
k = k + 1;
}
cout << m;
return 0;
}
d) Scrieţi în pseudocod un algoritm, echivalent cu cel dat, care să conțină o singură instrucțiune repetitivă.
citeşte n(număr natural) p <- 1; m <- 0; k <- 0 cât timp n≠0 execută --- citește x (număr natural) --- x <- [x/p] --- dacă x≠0 atunci c <- x%10 ------ altfel c <- n%10 --- m <- c * p + m --- n <- [n/10] --- p <- p*10; k <- k+1 scrie m
2. Variabila t memorează coordonatele reale (abscisa și ordonata), în planul xOy, ale fiecăruia dintre cele trei vârfuri A, B şi C ale unui triunghi. Știind că expresiile C/C++ de mai jos au ca valori abscisa vârfului A respectiv ordonatele vârfurilor B și C ale triunghiului, scrieți definiția unei structuri cu eticheta triunghi, care permite memorarea datelor precizate, și declarați corespunzător variabila t.
t.A.x. t.B.y t.C.y
struct triunghi
{
struct coord
{
double x, y;
} A, B, C;
} t;
3. În secvenţa alăturată, variabila a memorează un şir cu cel mult 100 de caractere, iar variabilele i şi k sunt de tip întreg. Scrieţi ce se afișează pe ecran în urma executării secvenţei.
k = ’a’ - ’A’;
strcpy(a, ”VIcToriE”);
cout << strlen(a);
for(i =0; i < strlen(a); i++)
if(a[i] >= ’A’ && a[i] <= ’Z’)
a[i] = a[i] + k;
else
a[i] = a[i] - k;
cout << a;
In k retinem un lucru foarte important. Retinem diferenta dintre o litera mica si o litera mare conform tabelului ascii – si anume 32. Mai departe, for-ul parcurge fiecare caracter al cuvantului si le transforma pe rand astfel: litera mare o face mica, iar litera mica o face mare.
Drept urmare, rezultatul este: 8 viCtORIe
Subiectul III.
1. Subprogramul putere are trei parametri:
- n, prin care primește un număr natural din intervalul [1,109];
- d și p, prin care furnizează divizorul prim, d, care apare la cea mai mare putere, p, în descompunerea în factori primi a lui n; dacă există mai mulți astfel de divizori se afișează cel mai mare dintre ei.
Scrieți definiția completă a subprogramului.
Exemplu: dacă n=10780, atunci, în urma apelului, d=7 şi p=2 (10780=22*5*72*11).
Pentru rezolvarea acestei probleme vom folosii algoritmul pentru descompunerea unui numar in factori primi. Pe masura ce descompunem numarul, verificam daca puterea este mai mare decat puterea maxima, si o inlocuim in pmax. La final atribuim lui d si p valorile lui dmax si pmax;
void putere(unsigned int n, unsigned int &d, unsigned int &p)
{
d = 2;
p = 0;
unsigned int dmax, pmax = 0;
while(n > 1)
{
while(n % d == 0)
{
n = n / d;
p = p + 1;
}
if(p != 0)
{
if(p >= pmax)
{
pmax = p;
dmax = d;
}
}
d = d + 1;
p = 0;
}
d = dmax;
p = pmax;
}
2. Scrieţi un program C/C++ care citeşte de la tastatură două numere naturale din intervalul [2, 20], n și k, şi construieşte în memorie un tablou bidimensional cu n linii şi n*k coloane, numerotate începând cu 1, astfel încât fiecare linie i (i∈[1,n]) memorează un şir crescător de termeni cu proprietatea că primul termen este i, fiecare valoare apare în şir de exact k ori și oricare doi termeni alăturați au valori egale sau consecutive.
Programul afişează pe ecran tabloul construit, fiecare linie a tabloului pe câte o linie a ecranului, cu valorile aflate pe aceeaşi linie separate prin câte un spaţiu.
Exemplu: dacă n=4 și k=3, se afişează pe ecran tabloul alăturat.
#include <iostream>
using namespace std;
int main()
{
unsigned int n, k, matrice[21][21], p = 1;
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
for (int j = 0; j < n; j++)
{
for (int kk = 1; kk <= k; kk++)
{
matrice[i][p] = j + i;
p = p + 1;
}
}
p = 1;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= k * n; j++)
cout << matrice[i][j] << " ";
cout << "\n";
}
return 0;
}
3. Se consideră șirul 1, 1, 2, 5, 13, 34, 89, 233, 610 ….
definit astfel: f1=f2=1, fn=3 * fn-1– fn-2 (unde n este un număr natural n≥3):
Se citesc de la tastatură două numere naturale x și y (x≤y≤109), valorile a doi termeni aflați pe poziții consecutive în şirul dat, şi se cere să se scrie în fişierul text bac.txt, în ordine descrescătoare, separați prin câte un spațiu, toţi termenii şirului care sunt mai mici sau egali cu y. Proiectați un algoritm eficient din punctul de vedere al memoriei utilizate şi al timpului de executare.
Exemplu: dacă se citesc numerele 89 233 fişierul bac.txt conţine numerele 233 89 34 13 5 2 1 1
a. Scrieți programul C/C++ corespunzător algoritmului proiectat.
b. Descrieți în limbaj natural algoritmul proiectat, justificând eficiența acestuia.
#include <iostream>
using namespace std;
int main()
{
unsigned int a, b, c = 0;
cin >> a >> b;
cout << b << " " << a << " ";
while(c != 1)
{
c = 3 * a - b;
cout << c << " ";
b = a;
a = c;
}
cout << 1;
return 0;
}
b. Algoritmul este eficient din punct de vedere al timpului, avand o complexitate liniara O(n) unde n este numarul total de elemenete generate. De asemenea, algoritmul are o complexitate constanta O(1) in spatiu, folosind doar variabile ce sunt strict necesare pentru rezolvarea problemei. Prima oara citesc cele doua numere de la tastatura, iar mai apoi generez urmatorul element prin inmultirea primului cu 3, scazand mai apoi ultimul element din acesta. In momentul cand am intalnit numarul 1, opresc generarea celorlalte elemente.