Componente tare conexe – Algoritmul lui Kosaraju in C++

Astazi vom vorbii despre componentele tare (sau tari?) conexe ale unui graf orientat, rezolvand problema ctc – infoarena.ro.

Ce este o componenta tare conexa?

In Teoria Grafurilor, o componenta este tare conexa daca poti ajunge dintr-un nod in oricare alt nod. Insa aceste componente tare conexe pot forma mai multe sub-partitii care sunt conectate intre ele. (vezi exemplul de mai jos)

In acest graf orientat avem 3 componente tare conexe.

• Componenta 1: 1, 2, 3
• Componenta 2: 4, 5
• Componenta 3: 6, 7, 8

Putem observa cum cele 3 componente conexe sunt la randul lor, accesibile intre ele.

Definitie: G1 = (V1, E1) este o componenta tare conexa daca:

• pentru orice pereche x, y de varfuri din V1 exista un drum de la x la y si drum de la y la x
• nu exista alt subgraf al lui G, G2=(V2, E2) care sa indeplineasca prima conditie si care sa-l contina pe G1

Proprietatile unei componente conexe:

• Doua componente conexe C1 si C2 sunt doua multimi disjuncte sau doua multimi egale intre ele.
• Fiecare nod apartine exact unei singure componente conexe

Problema CTC – infoarena.ro

Pentru a intelege mai bine componentele conexe vom rezolva problema ctc de pe infoarena.ro: click.

Enunt: Dandu-se un graf orientat G = (V, E) se cere sa se determine componentele sale tare conexe.

Avem mai sus exemplul din problema, desenat si observam ca sunt doua componente conexe in total. Pentru a rezolva acest tip de problema exista doi algoritmi: algoritmul lui Kosaraju si algoritmul lui Tarjan.

Algoritmul lui Kosoraju

Algoritmul lui Kosoraju este urmatorul:

• Pasul 1: Creeaza o stiva goala “S” si parcurge graful printr-un DFS. In momentul cand te intorci din parcurgerea recursiva (“zona 4” din DFS – vorbim despre asta mai jos) – pune nodul in stiva. De exemplu, in problema de mai sus obtinem stiva: 7 4 8 5 6 3 2 1 (unde 1 este ultimul element introdus in stiva).
• Pasul 2: Inversam directiile grafului pentru a construi transpusa acestuia.
  

  Inversa grafului din problema

• Pasul 3: Scoate cate un element rand pe rand din stiva “S”. Daca elementul selectat nu a mai fost vizitat, porneste o parcurgere DFS in graful construit la pasul 2. De fiecare data cand vom porni un DFS vom avea o noua componenta conexa.

Algoritmul lui Kosoraju – Cum functioneaza?

In exemplul de pe Wikipedia se explica cel mai bine cum sta treaba.

Avem in figura de mai sus un graf format din punctuletele mici albastre. Daca condensam graful (ne uitam la punctele galbene) – observam faptul ca acesta devine un graf orientat aciclic. Acelasi lucru se intampla si in exemplul problemei noastre, obtinem graful acilic:

(patratul albastru reprezinta un nod iar patratul mov reprezinta alt nod)

Teorema: Pentru orice graf orientat G, in momentul cand il condensam, obtinem un graf aciclic ( demonstratia – aici. )

Asadar, ajungem la urmatoarea observatie: componentele tare conexe dintr-un graf formeaza intre ele un graf orientat aciclic. Daca abstractizam putin teorema, putem sa gandim graful pe doua nivele. Primul nivel este reprezentat de componentele tare conexe din graful aciclic (nodurile galbene / dreptunghiurile), iar cel de-al doilea nivel este reprezentat de nodurile ce formeaza fiecare componenta conexa.

O operatie utila atunci cand vine vorba de grafuri orientate aciclice este sortarea topologica. Deoarece aceasta ne garanteaza ca daca exista un arc (i, j), atunci i apare inaintea lui j in aceasta sortare.

Sortand topologic graful de mai sus, obtinem stiva de elemente scrisa sub acesta. Putem observa faptul ca pornind pe rand cate un DFS din fiecare nod, putem determina componentele conexe ale acestuia.

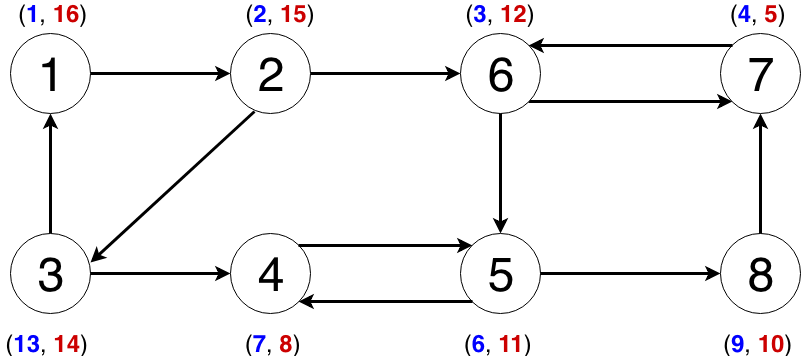Avem aici graful din problema. De-asupra fiecarui nod se gaseste timpul in care s-a pornit un DFS din acesta (numarul albastru) si timpul in care s-a incheiat un DFS din acesta (numarul visiniu). Asadar, sortand timpii de finish, obtinem stiva formata din nodurile 7 4 8 5 6 3 2 1.

Daca parcurgem transpusa grafului printr-un DFS (pornind din nodul 1), observam faptul ca acesta determina cate o componenta conexa. (inversand sensul grafului ti se garanteaza faptul ca o parcurgere DFS determina componenta conexa).

Algoritmul in C++

#include    <fstream>
#include    <iostream>
#include    <vector>
#include    <stack>

#define NMax 100005

using namespace std;

ifstream fin("ctc.in");
ofstream fout("ctc.out");

stack < int > S;

vector<int> G[NMax],GT[NMax],CTC[NMax];

int N, M, NrCTC;
int beenThere[NMax];

void Read()
{
    fin >> N >> M;
    for(int i = 1; i <= M; i++)
    {
        int x,y;
        fin >> x >> y;
        G[x].push_back(y); // Construim graful G
        GT[y].push_back(x); // Construim transpusa grafului G
    }
}

void DFSP(int Nod)
{
    beenThere[Nod] = 1;
    for(unsigned int i=0; i<G[Nod].size();i++) {
        int Vecin = G[Nod][i];

        if(!beenThere[Vecin])
            DFSP(Vecin);
    }
    S.push(Nod);
}

void DFSM(int Nod)
{
    beenThere[Nod] = 2;
    CTC[NrCTC].push_back(Nod);

    for(unsigned int i=0; i<GT[Nod].size();i++) {
        int Vecin = GT[Nod][i];

        if(beenThere[Vecin]==1)
            DFSM(Vecin);
    }
}

void Solve()
{
    for(int i=1;i<=N;i++)
        if(!beenThere[i])
            DFSP(i);

    while(!S.empty()) {
        int Nod = S.top();
        cout << Nod << " ";
        if (beenThere[Nod] == 1) {
            NrCTC++;
            DFSM(Nod);
        }
        S.pop();
    }
}

void Print()
{
    fout << NrCTC <<"\n";

    for(int i = 1; i <= NrCTC; i++) {
        for(unsigned int j = 0; j < CTC[i].size(); j++)
            fout << CTC[i][j] <<" ";
        fout<<"\n";
    }
}

int main()
{
    Read();
    Solve();
    Print();
    return 0;
}