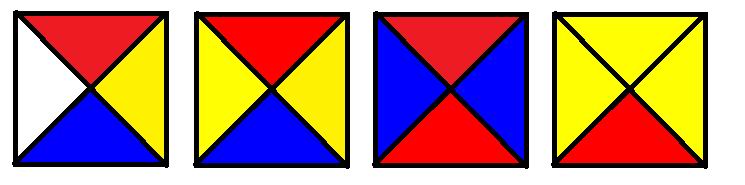
Gigel vrea să confecţioneze un ornament pentru pomul de iarnă format din pătrăţele frumos colorate. Pătrăţelele pot arăta ca în desenul alăturat. Se observă faptul că ele pot avea 4 culori diferite pe cele 4 laturi, 3, 2 sau chiar o singură culoare pe toate cele 4 laturi ale pătrăţelului.
Gigel are la dispoziţie n (n pătrat perfect) pătrăţele egale de acest tip cu laturile colorate doar în patru culori (alb, roşu, galben, albastru). Le vom numerota simplu de la 1 la 4.
Cerința
Să se scrie un program care primeşte o listă de n pătrăţele colorate şi determină o aranjare a lor sub forma de pătrat de forma k•k (k•k = n) astfel încât două laturi adiacente să aibă aceeaşi culoare, precum şi numărul de astfel de aranjări.
Date de intrare
Fişierul de intrare ornament.in va conţine pe prima linie valoarea n. Următoarele n linii vor conţine câte patru numere naturale N, E, S, V separate prin câte un spaţiu, reprezentând cele 4 culori ale laturilor pătrăţelelor. Ordinea laturilor este considerată: Nord, Est, Sud, Vest şi pătrăţelele nu se vor roti. Ultima linie din fişierul de intrare va conţine una dintre valorile 1 sau 2; valoarea 1 indică faptul că este cerută o soluţie corectă, iar valoarea 2 indică faptul că este cerut numărul de soluţii corecte.
Date de ieșire
În cazul cerinţei 1 fişierul de ieşire ornament.out va conţine k linii. Fiecare linie va conţine câte k valori reprezentând numerele de ordine ale pătrăţelelor din fişierul de intrare, aranjate astfel încât să fie respectată condiţia din enunţ. În cazul cerinţei 2, fişierul de ieşire va conţine pe prima linie un singur număr natural reprezentând numărul de soluţii corecte.
Restricții și precizări
• n = 4, 9, 16
Gigel vrea să confecţioneze un ornament pentru pomul de iarnă format din pătrăţele frumos colorate. Pătrăţelele pot arăta ca în desenul alăturat. Se observă faptul că ele pot avea 4 culori diferite pe cele 4 laturi, 3, 2 sau chiar o singură culoare pe toate cele 4 laturi ale pătrăţelului.
Gigel are la dispoziţie n (n pătrat perfect) pătrăţele egale de acest tip cu laturile colorate doar în patru culori (alb, roşu, galben, albastru). Le vom numerota simplu de la 1 la 4.

Cerința
Să se scrie un program care primeşte o listă de n pătrăţele colorate şi determină o aranjare a lor sub forma de pătrat de forma k•k (k•k = n) astfel încât două laturi adiacente să aibă aceeaşi culoare, precum şi numărul de astfel de aranjări.
Date de intrare
Fişierul de intrare ornament.in va conţine pe prima linie valoarea n. Următoarele n linii vor conţine câte patru numere naturale N, E, S, V separate prin câte un spaţiu, reprezentând cele 4 culori ale laturilor pătrăţelelor. Ordinea laturilor este considerată: Nord, Est, Sud, Vest şi pătrăţelele nu se vor roti. Ultima linie din fişierul de intrare va conţine una dintre valorile 1 sau 2; valoarea 1 indică faptul că este cerută o soluţie corectă, iar valoarea 2 indică faptul că este cerut numărul de soluţii corecte.
Date de ieșire
În cazul cerinţei 1 fişierul de ieşire ornament.out va conţine k linii. Fiecare linie va conţine câte k valori reprezentând numerele de ordine ale pătrăţelelor din fişierul de intrare, aranjate astfel încât să fie respectată condiţia din enunţ. În cazul cerinţei 2, fişierul de ieşire va conţine pe prima linie un singur număr natural reprezentând numărul de soluţii corecte.
Restricții și precizări
• n = 4, 9, 16
• Pentru datele de intrare problema are întotdeauna soluţie, în timpul indicat.
Exemplul 1:
ornament.in
16 4 4 1 1 4 3 1 2 2 2 2 3 4 1 3 2 1 1 3 1 1 3 1 1 2 4 1 3 3 1 1 4 3 2 4 1 1 3 2 2 1 4 4 3 1 1 2 4 4 3 3 2 2 1 1 3 4 4 3 1 2 4 4 4 1
ornament.out
2 3 4 9 10 7 8 1 16 12 6 11 13 14 5 15
Explicație
Soluţia corespunde aranjării
|-4-| |-2-| |-4-| |-3-| 2 3 3 2 2 1 1 2 |-1-| |-2-| |-3-| |-4-| |-1-| |-2-| |-3-| |-4-| 2 3 3 4 4 1 1 4 |-2-| |-1-| |-1-| |-1-| |-2-| |-1-| |-1-| |-1-| 4 4 4 1 1 3 3 4 |-4-| |-2-| |-1-| |-4-| |-4-| |-2-| |-1-| |-4-| 2 3 3 1 1 1 1 4 |-3-| |-1-| |-3-| |-3-|
Exemplul 2:
ornament.in
16 4 4 1 1 4 3 1 2 2 2 2 3 4 1 3 2 1 1 3 1 1 3 1 1 2 4 1 3 3 1 1 4 3 2 4 1 1 3 2 2 1 4 4 3 1 1 2 4 4 3 3 2 2 1 1 3 4 4 3 1 2 4 4 4 2
ornament.out
1
Explicație
#include <bits/stdc++.h>
using namespace std;
ifstream cin("ornament.in");
ofstream cout("ornament.out");
struct poz
{
int N , E , S , V;
}a[20];
int x[6][6] , n , m , p[20] , cer , nrsol , gata;
void afisare()
{
if(cer == 2) nrsol++;
else
{
for(int i = 1 ; i <= m ; i++)
{
for(int j = 1 ; j <= m ; j++)
cout << x[i][j] << " ";
cout << '\n';
}
gata = 1;
}
}
int verifica(int l , int c)
{
if(c > 1) if(a[x[l][c - 1]].E != a[x[l][c]].V) return 0;
if(l > 1) if(a[x[l - 1][c]].S != a[x[l][c]].N) return 0;
return 1;
}
void back(int l , int c)
{
for(int i = 1 ; i <= n && !gata; i++)
if(!p[i])
{
p[i] = 1;
x[l][c] = i;
if(verifica(l , c))
if(l == m && c == m) afisare();
else if(c < m) back(l , c + 1);
else back(l + 1 , 1);
p[i] = 0;
}
}
int main()
{
cin >> n;
m = sqrt(n);
for(int i = 1 ; i <= n ; i++)
cin >> a[i].N >> a[i].E >> a[i].S >> a[i].V;
cin >> cer;
back(1 , 1);
if(cer == 2) cout << nrsol;
}