Distanta dintre doua puncte in geometrie

Fie xOy un sistem cartezian ortogonal si fie A(x_A,y_A), B(x_B,y_B) doua puncte din acest  sistem. Formula de calcul a distantei dintre cele doua puncte , de altfel si formula de calcul a lungimii unui segment este urmatoarea:

Formula distanta dintre doua puncte

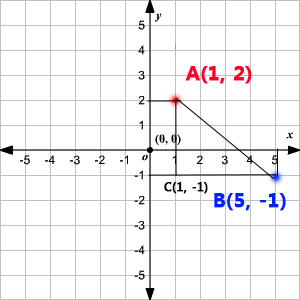
Pentru a demonstra aceasta formula, vom analiza poza de mai jos:

Distanta dintre doua puncte

Avem doua puncte: A(1, 2) si B(5, -1). Deci avem urmatoarele valori:

• A(1, 2) -> X_A = 1 Y_A = 2
• B(5, -1) -> X_B = 5 Y_B = -1

Daca inlocuim in formula de mai sus vom obtine lungimea AB = 5

Haideti sa mai tragem cateva linii suplimentare.

Demonstratia formulei

Am trasat proiectile celor doua puncte pe axa Ox si axa Oy. Dupa care am prelungit acele proiectii pentru a forma triunghiul dreptunghic ACB. Acest triunghi are laturile AC = 3 si BC = 4, deoarece:

Lungimea segmentului AC

Lungimea segmentului BC

Pentru a calcula ipotenuza AB (care este totodata distanta dintre punctul A si punctul B), aplicam Teorema lui Pitagora, astfel incat:

Calculul distantei dintre doua puncte in C++

#include    <iostream>
#include    <cmath>

using namespace std;

int main()
{
    int X_A, Y_A;
    int X_B, Y_B;

    cout << "Introdu coordonatele punctului A: ";
    cin >> X_A >> Y_A;

    cout << "Introdu coordonatele punctului B: ";
    cin >> X_B >> Y_B;

    cout << "Distanta dintre cele doua puncte este: ";
    float distanta = sqrt(((X_A - X_B) * (X_A - X_B)) + ((Y_A - Y_B) * (Y_A - Y_B)));
    cout << distanta;

    return 0;
}