De ce este utila aceasta notiune?
In acest tutorial vom discuta despre ce este complexitatea. Acest concept te va ajuta in viitor sa iti dai seama cat timp ii ia programului tau sa ruleze atunci cand numarul de date este foarte mare.
Timpul de rulare poate fi influentat de mai multi factori, precum: ce procesor ai, cata memorie RAM, ce viteza de scriere si citire are sistemul de stocare, s.a.m.d. Asadar, programatorilor le trebuie o metoda comuna prin care sa stabileasca cat de eficienti sunt algoritmii.
Eficienta unui algoritm
Pentru a intelege mai bine de ce este nevoie sa cunoastem aceasta notiune, vom lua urmatoarea problema simpla drept exemplu: Catalin si Paul doresc sa stie daca un numar dat (N) este prim. Din pacate, cei doi au un mod diferit de a determina daca un numar este prim, sau nu.
Ce este un numar prim? Un numar prim este un numar care se imparte doar la 1 si la el insusi. Atentie: 1 nu este numar prim (de ce? citeste propozitia urmatoare mai atent).
Metoda lui Catalin: foloseste un for ca sa ia toate numerele de la 2 pana la N / 2 si verifica daca are loc impartirea exacta (fara rest). In momentul cand aceasta are loc, inseamna ca numarul nu este prim.
bool ePrim = true;
for(int div = 2; div <= N / 2; div++)
{
if(N % div == 0)
{
ePrim = false;
break;
}
}
cout << "N este prim: " << ePrim;
Metoda lui Paul: foloseste un for ca sa ia toate numerele de la 2 pana la radical din N sii verifica daca are loc impartirea exacta (fara rest). In momentul cand aceasta are loc, inseamna ca numarul nu este prim.
bool ePrim = true;
for(int div = 2; div <= sqrt(N); div++)
{
if(N % div == 0)
{
ePrim = false;
break;
}
}
cout << "N este prim: " << ePrim;
Sa presupunem faptul ca domnul Calculator are nevoie de 1 ms (milisecunda) pentru a calcula o operatie de genul N % div. Vom analiza eficienta acestui algoritm pentru cel mai rau caz (cazul in care nu gasim nici un divizor, iar numarul este prim).
Pentru N = 11 / N = 101 / N = 10,000,000,019 (1010 + 19)
- Catalin: 5 ms / 50 ms / 5 * 109 ms (~115 zile)
- Paul: 3 ms / 10 ms / 105 ms (~2 min)
Haideti sa reprezentam acest timp de rulare folosind un grafic.
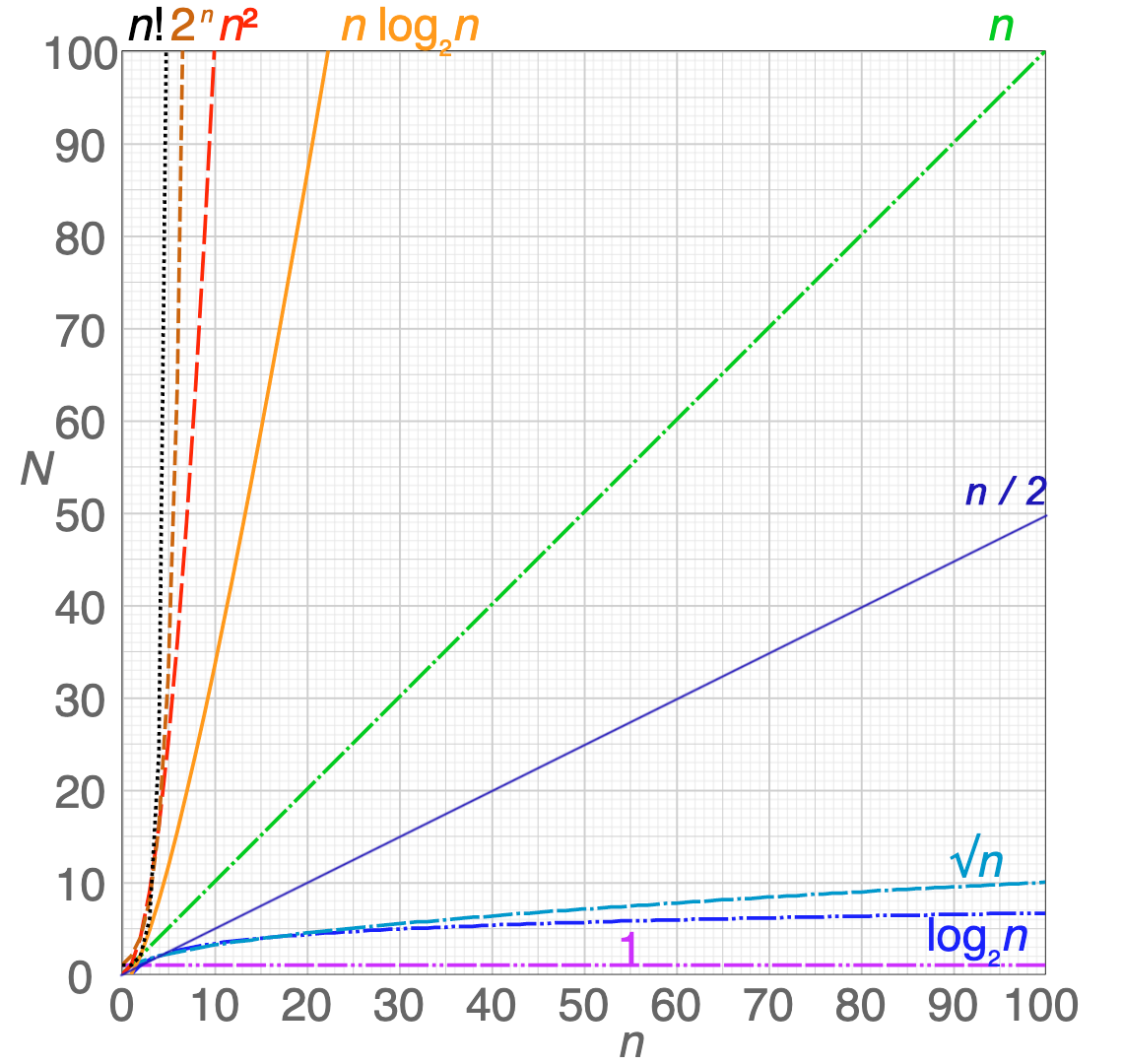Puteti vedea cum timpul de rulare pentru algoritmul lui Catalin “creste” mai mult pe masura ce numarul primit este mai mare. In schimb, algoritmul lui Paul nu se “departeaza” foarte mult de orizontala.
Ce este complexitatea unui algoritm?
In informatica, complexitatea unui algoritm masoara cat de repede creste timpul pe masura ce marimea input-ului se mareste. Analizand graficul de mai sus, un algoritm care se aproprie foarte mult de axa Oy este considerat ineficient, iar un algoritm care este mai aproape de axa Ox este considerat eficient.
Complexitatea poate fi:
- constanta – O(1)
- logaritmica – O(log2n)
- liniara – O(n)
- patratica – O(n2)
- polinomiala – O(nk)
Complexitatea unui algoritm in timp
Pentru a intelege mai bine, vom atribuii urmatorilor algoritmi cate “1 punct” pentru fiecare operatie. Mai departe vom descrie procedeul prin care calculezi complexitatea in timp:
- Aduni “toate punctele” (explicatie mai amanuntita in video)
- Selectezi termenul care creste cel mai rapid
- Stergi coeficientul
De exemplu, daca, Tr (timpul de rulare) este:
- T = a (unde a este constant), atunci complexitatea va fi O(1)
- T = an + b (unde a si b sunt constante), atunci complexitatea va fi O(n) (pentru ca doar n este o necunoscuta ce creste pe masura ce primim valori)
- T = bn2 + an + c (unde a, b si c sunt constante), atunci complexitatea algoritmului va fi O(n2) (pentru ca n2 creste cel mai rapid dintre toti)
Complexitate constanta – O(1)
Sa luam functia care calculeaza suma a doua numere, a si b.
int a, b; cin >> a >> b; cout << a + b;
Conform regulii de mai sus, acest algoritm va avea “1 punct. deoarece a facut o operatie. Daca aveam 10 numere (a, b, c, d, …) atunci algoritmul aveam “9 puncte”. Aplicand regula de inainte, calculam complexitatea, dar nu avem nici un termen care ar influenta rata de crestere a algoritmului, asadar acesta este constant.
Complexitate liniara – O(n)
Sa luam acum, un algoritm putin mai diferit, si vom calcula suma elementelor unui vector.
int n = 7, suma = 0;
int V[] = {42, 86, 17, 25, 15, 63, 12};
for(int i = 0; i < n; i++)
suma = suma + V[i];
cout << "Suma este: " << suma;
In momentul cand parcurgem n elemente dintr-un vector, vom efectua n operatii, asadar avem “n puncte”. Aplicand regulile dinainte, vom avea complexitatea O(n) unde n reprezinta numarul total de elemente din vector.
Sa luam alt algoritm in schimb, sa presupunem ca avem doi vectori.
int n = 7, m = 5, suma = 0;
int V[] = {42, 86, 17, 25, 15, 63, 12};
for(int i = 0; i < n; i++)
suma = suma + V[i];
int U[] = {420, 18, 58, 12, 1};
for(int i = 0; i < m; i++)
suma = suma + U[i];
cout << "Suma este: " << suma;
In acest caz, dupa ce calculam punctele obtinem O(n + m), dar aplicand cele trei reguli de mai sus, scoatem numarul m din calcul (deoarece trebuie sa selectez doar cel care creste cel mai rapid – iar amandoi cresc la fel de rapid), si obtinem complexitatea O(n).
Complexitate patratica – O(n2)
Iar acum vom lua un alt exemplu, sa presupunem ca dorim sa aflam produsul cartezian a doi vectori. Vom avea urmatorul algoritm:
int n = 3, m = 2;
int V[] = {42, 86, 17};
int U[] = {420, 18};
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
cout << "(" << V[i] << ", " << U[j] << ")\n";
}
Adunand punctele, observam ca avem un total de n * m, asadar complexitatea acestui algoritm este O(n*m), iar daca m = n, complexitatea devine una patratica – adica O(n2).
In concluzie, pentru a calcula complexitatea unui algoritm, trebuie sa calculam pe rand cate puncte “obtine” fiecare particica mai mica din acesta. Pe masura ce spargem problema noastra in probleme mai mici, vom calcula “totalul punctelor”, iar mai apoi vom aplica regulile de mai sus pentru a determina complexitatea in timp a acestuita. Asadar, de-acum in-colo cand cineva o sa va intrebe: “cat de rapid este algoritmul tau?” ii vei raspunde “are o complexitate liniara in timp” cu in loc de “merge sub 2 secunde”.
