Determinarea unui subsir de suma maxima
In acest tutorial o sa discutam despre algoritmul lui Kadane si ce problema incearca acesta sa rezolve. Sa luam urmatoarea problema drept exemplu:
Se da un șir de cel mult 106 numere întregi din intervalul [-103,103], separate prin
câte un spațiu. Se cere să se afișeze pe ecran suma maximă obținută adunând numere de pe poziții
consecutive în șirul aflat în fișier.
Exemplu: dacă avem valorile 4 -6 7 2 -1 4 -10 -3 se afișează pe ecran numărul 12
Ce este un subsir?
Un subsir este un sir continuu ce se afla in interiorul sirului nostru principal. Reprezentand numerele din problema, putem identifica urmatoarele subsiruri:
- Subsirul 7, 2
- Subsirul format doar din elementul -6
- Subsirul 2, -1, 4
Atentie: elementele dintr-un subsir trebuie sa se afle unul dupa celalalt, asadar subsirul format din elemntele 2 si -10 nu este valid, deoarece 2 se afla pe pozitia 3 iar -10 pe pozitia 6.
Revenind la problema, daca ne uitam la multimea de mai sus, subsirul format din 7, 2, -1 si 4 formeaza subsirul de suma maxima (12).
Metoda brute-force O(n2)
Probabil prima metoda ce va trece prin cap este metoda brute-force. Pentru fiecare element, calculam suma pentru fiecare subsir ce incepe din acesta.
De exemplu: luam sirul format din 4, -6 dupa care, sirul format din 4, -6, 7, dupa care 4, -6, 7, 2 si asa mai departe. Insa aceasta metoda are o complexitate destul de ridicata.
Va las mai jos codul folosind aceasta metoda, daca doriti sa experimentati putin cu el.
#include <iostream>
using namespace std;
int main()
{
int v[10] = {4, -6, 7, 2, -1, 4, -10, -3};
int n = 8;
int sumaMax = 0;
for(int i = 0; i < n; i++)
{
int suma = 0;
for(int j = i + 1; j < n; j++)
{
suma = suma + v[j];
if(suma > sumaMax)
sumaMax = suma;
}
}
cout << sumaMax;
return 0;
}
Algoritmul lui Kadane O(n)
Solutia cea mai buna pentru aceasta problema este cunoscuta in informatica drept: Algoritmul lui Kadane. Haideti sa analizam ideea din spatele acestui algoritm mai intai: ne vom uita mai intai la fiecare indice si analizam care este subsirul de suma maxima care se termina in acel indice.
Asadar, pentru primul indice, subsirul de suma maxima este 4. Iar pentru
- i = 1, subsirul de suma maxima poate sa fie [0, 1] sau [1]
- i = 2, subsirul de suma maxima poate sa fie [0, 1, 2], [1, 2] sau [2]
- i = 3, subsirul de suma maxima poate sa fie [0, 1, 2, 3], [1, 2, 3], [2, 3] sau [3]
- s.a.m.d.
Sa simplificam putin problema, vom lua doar primele trei elemente:
 Luam elementul de pe indicele 2. Subsirul de lungime maxima care se termina in indicele 2 poate sa fie:
Luam elementul de pe indicele 2. Subsirul de lungime maxima care se termina in indicele 2 poate sa fie:
- elementul insusi (7) sau
- elementul insusi adunat cu suma maximala din subsirul anterior (adica [0, 1] + [2])
Comparam cele doua variante si avem de ales intre 7 sau 5 (4 – 6 + 7) .
De ce functioneaza? Explicatia

Sa spunem ca avem un element x ce se afla pe pozitia i, si de asemenea cunoastem suma maxima a subsirului precedent (subsir ce il vom nota cu A – in acest subsir se pot afla orice elemente). Asadar, subsirul de lungime maxima care se termina in i, poate sa fie:
- elementul insusi (x)
- elementul insusi adunat cu A.
Vom demonstra aceasta rezolvare folosind metoda falsei ipoteze. Sa presupunem ca suma maxima nu este formata din elementele lui A, vom spune ca suma maxima poate fi formata din elementele altui subsir notat cu B. Asadar B:
- este diferit de multimea vida
- poate sa fie mai mare ca A
- poate sa fie mai mic ca A
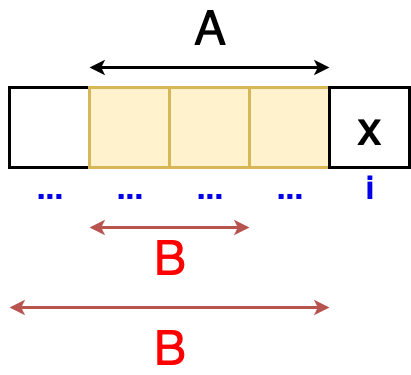 Vom nota cu sumMax(A, x) = suma maxima a elementelor din A + elementul x
Vom nota cu sumMax(A, x) = suma maxima a elementelor din A + elementul x
Presupunem ca exista sumMax(B, x) astfel incat sumMax(B, x) > sumMax(A, x)
- sumMax(B, x) = sumMax(B) + x
- sumMax(A, x) = sumMax(A) + x
- sumMax(B) > sumMax(A)
Dar asta contrazice ideea prezentata mai devreme, deoarece am notat cu sumMax(A) suma maxima a elementelor ce se termina pe pozitia i – 1. Asadar, nu pot exista doua sume maxime simultan. Exista doar un singur maxim.
Algoritmul arata in felul urmator:
#include <iostream>
using namespace std;
int main()
{
int v[10] = {4, -6, 7, 2, -1, 4, -10, -3};
int n = 8;
int suma = 0, sumaMax = 0;
for(int i = 0; i < n; i++)
{
suma = suma + v[i];
if(suma < 0)
suma = 0;
if(suma > sumaMax)
sumaMax = suma;
}
cout << sumaMax;
return 0;
}
Iar acum sa urmarim algoritmul pas cu pas pentru fiecare element:

