Ce este cautarea binara?

Algoritmul de cautare binara este un algoritm folosit pentru a gasii un elemnt intr-o lista ordonata (crescatoare sau descrescatoare). Algoritmul foloseste tehnica „divide et impera” (sau „divide si cucereste” pe romana). Deoarece dupa fiecare pas, cardinalul multimii se injumatateste, acest algoritm are o complexitate logaritmica. Citeste mai multe: Cautarea binara – Wikipedia

Algoritmul pentru cautarea binara

Se da un sir de numere ordonat crescator cu N elemente, se cere sa se returneze pozitia in sir a unui numar introdus de la tastatura.

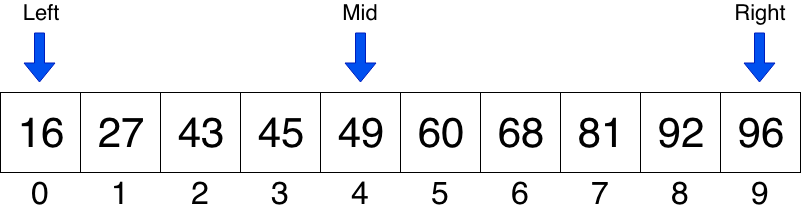
Consideram deja ca avem vectorul V cu cele N elemente ordonate crescator. Ne alegem trei variabile, pe care eu le voi denumii: Left, Right si Mid.

• Left – inceputul intervalului in care cautam
• Mid – mijlocul intervalului
• Right – sfarsitul intervalului in care cautam

Algoritmul verifica de mai multe ori daca Mid este egal cu valoarea elementului cautat de noi. Numai ca intervalul se modifica pe masura ce algoritmul ruleaza.

• In cazul in care V[Mid] == x (unde x – este elementul cautat de noi) – algoritmul a gasit elementul cautat de noi
• In caz contrar:
  • daca x este mai mic decat V[Mid], Right va devenii Mid
  • daca x este mai mare decat V[Mid], Left va devenii Mid

Tot ceea ce am descris mai sus se repeta atata timp cat Left <= Right.

Cautarea binara in C++

Varianta 1 (clasica):

#include    <iostream>

using namespace std;

const int N = 10;

int V[N] = {16, 27, 43, 45, 49, 60, 68, 81, 92, 96};

int CautareBinara(int x)
{
    int Sol = -1, Left = 0, Right = N;
    while(Left <= Right)
    {
        int Mid = (Left+Right) / 2;
        if(V[Mid] == x)
        {
            Sol = Mid;
            break;
        }
        if(V[Mid] > x)
            Right = Mid - 1;
        if(V[Mid] < x)
            Left = Mid + 1;
    }
    return Sol;
}

int main()
{
    cout << CautareBinara(43);
    return 0;
}

Varianta 2 (recursiva):

#include    <iostream>

using namespace std;

const int N = 10;

int V[N] = {16, 27, 43, 45, 49, 60, 68, 81, 92, 96};

int CautareBinara(int Left, int Right, int x)
{
    if(Left > Right)
        return -1;
    else
    {
        int Mid =(Left+Right)/2;
        if(x == V[Mid])
            return Mid;
        if(x < V[Mid])
            return CautareBinara(Left, Mid-1, x);
        else
            return CautareBinara(Mid+1, Right, x);
    }
}

int main()
{
    cout << CautareBinara(0, N-1, 43);
    return 0;
}

Varianta 3 (folosind upper_bound()):

#include    <algorithm>
#include    <iostream>

using namespace std;

const int N = 10;

int V[N] = {16, 27, 43, 45, 49, 60, 68, 81, 92, 96};

int main()
{
    int value = 43;
    int result = upper_bound(V, V+N, value) - V - 1;
    if(result >= 1 && result <= N && V[result] == value)
        cout << result;
    else
        cout << -1;
    return 0;
}

Desfasurarea algoritmului de cautare binara pas cu pas:

Pasul initial: Sol: -1 Left: 0 Right: 9
Pasul 1: Sol: -1 Left: 0 Right: 3
Pasul 2: Sol: 2 Left: 2 Right: 3

Avem Left = 0, Right = 9, Mid = 4. Daca inlocuim V[Mid] = 49. Deoarece 49 > 43, Right devine 3.

Avem Left = 0, Right = 3, Mid = 1. Daca inlocuim V[Mid] = 27. Deoarece 27 < 43, Left devine 2.

Avem Left = 2, Right = 3, Mid = 2. Daca inlocuim V[Mid] = 43, obtinand numarul cautat de noi.

Complexitatea algoritmului pentru cautarea binara

Pentru a calcula complexitatea acestui algoritm, vom construii un arbore. Radacina arborelui va fi elementul din mijloc. Mai apoi, copilul din stanga va fi mijlocul multimii din stanga, iar copilul din dreapta va fi mijlocul multimii din dreapta. Ca sa intelegeti mai bine, haideti sa desenam copacul multimii noastre:

In cel mai bun caz, algoritmul nostru gaseste elementul in O(1) – atunci cand elementul cautat se afla exact in mijlocul multimii.

In cel mai rau caz, cautarea binara efectueaza log₂(n) comparatii. Cel mai rau caz este obtinut atunci cand algoritmul nostru sapa pana la ultimul nivel al arobrelui. De asemenea, atunci cand elementul cautat nu se afla in multime, se executa tot log₂(n) comparatii.

Putem observa faptul ca dupa fiecare comparare, intervalul in care noi cautam se injumatateste. Sa presupunem ca aveam 16 elemente (pentru a simplifica calculele).

Din cate putem observa, exista o legatura stransa intre log₂(n) si numarul efectiv de cautari. Asadar, complexitatea acestui algoritm este O(log₂n).