Cerința

Se dau n și m reprezentând dimensiunile unui tablou bidimensional format din elementele 0 si 1. Se definește o parcelă ca fiind o grupare de elemente vecine cu valoarea 1, condiția de vecinătate dintre două elemente fiind ca, luat unul dintre ele ca referință, celălalt să fie deasupra, dedesupt, în stânga sau în dreapta acestuia. Parcele se numerotează parcurgând matricea de sus în jos și de la stânga la dreapta, astfel:

1. primul element din matrice egal cu 1 face parte din parcela numărul 1
2. primul element din matrice care este egal cu 1 și nu face face parte din parcela 1 face parte din parcela 2;
3. primul element din matrice care este egal cu 1 și nu face face parte din parcelele 1 și 2 face parte din parcela 3;
4. etc.

Să se determine numărul de parcele nr, aria maximă a unei parcele amax și respectiv numărul parcelei cu arie maximă pmax.

Date de intrare

Fișierul de intrare parcela.in conține pe prima linie numerele n și m, iar pe a doua linie un tablou bidimensional cu n×m elemente.

Date de ieșire

Fișierul de ieșire parcela.out va conține pe prima linie numerele nr amax pmax cu semnificațiile din enunț, separate prin câte un spațiu.

Restricții și precizări

• 1 ≤ n,m ≤ 100

Exemplu

parcela.in

5 6
0 1 1 1 0 1
0 0 1 0 0 1
0 1 0 0 0 1
0 0 0 0 1 1
1 1 1 0 0 1

parcela.out

4 6 2

Explicație

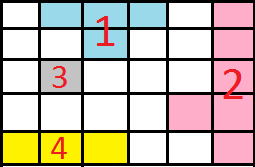
Există 4 parcele, numerotate ca în imaginea de mai jos. Aria maximă a unei parcele este 6, iar parcela corespunzătoare este parcela 2.

#include <bits/stdc++.h>
using namespace std;

ifstream cin("parcela.in");
ofstream cout("parcela.out");

int a[105][105];

void fill(int i , int j , int &c)
{
    if(a[i][j]==1)
    {
        a[i][j]=0;
        c++;
        if(a[i+1][j]==1)
            fill(i+1 , j , c);
        if(a[i-1][j]==1)
            fill(i-1 , j , c);
        if(a[i][j+1]==1)
            fill(i , j+1 , c);
        if(a[i][j-1]==1)
            fill(i , j-1 , c);
    }
}

int main()
{
    int n , m;
    cin >> n >> m;
    for(int i = 1 ; i <= n ; ++i)
        for(int j = 1 ; j <= m ; ++j)
            cin >> a[i][j];
    int cnt = 0 , max=0 , lmax=0;
    for(int i = 1 ; i <= n ; ++i)
        for(int j = 1 ; j <= m ; ++j)
            if(a[i][j]==1)
            {
                cnt++;
                int c = 0;
                fill(i , j , c);
                if(c > max)
                    max = c , lmax=cnt;
            }
    cout << cnt << ' ' << max << ' ' << lmax;
    return 0;
}