Cerinţa
Alice s-a pierdut din nou în labirint. Labirintul este de forma unui triunghi dreptunghic împărțit în camere organizate pe linii și coloane. Pe prima linie este o singură cameră, pe a doua sunt două camere, etc. Pe ultima linie sunt n camere. Din fiecare cameră se poate merge în camerele situate pe linia următoare și pe aceeași coloană, sau pe coloane cu 1 mai mari sau mai mici decât coloana curentă, dar fără să se părăsească labirintul. Astfel din camera (i,j) se poate merge în camerele (i+1,j-1), (i+1,j) și (i+1,j+1), dacă acestea există. Alice se află în camera de pe prima linia și de pe prima coloana (1,1).
Ca să iasă din labirint, Alice trebuie să ajungă într-o cameră de pe ultima linie. Calculați și afișați numărul de trasee pe care poate Alice să iasă din labirint.
Date de intrare
Fișierul de intrare alice_xi.in conține pe prima linie numărul n, reprezentând numărul de linii din labirint.
Date de ieşire
Fişierul de ieşire alice_xi.out va conţine pe prima linie numărul s, reprezentând numărul de trasee pe care poate Alice să iasă din labirint.
Restricţii şi precizări
1 ≤ n ≤ 35
Exemplu
alice_xi.in
3
alice_xi.out
5
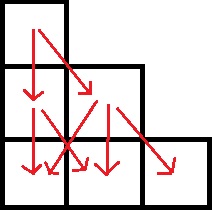
Explicație
Pe ultima linie sunt 3 camere. În prima se poate ajunge în 2 moduri, în cea de-a doua în 2 noduri, iar în a treia într-un singur mod. În total sunt 5 moduri în care se poate ajunge pe ultima linie.
#include <bits/stdc++.h>
using namespace std;
ifstream cin("alice_xi.in");
ofstream cout("alice_xi.out");
long long n , a[101][101] , sum;
int main()
{
cin >> n;
a[1][1] = 1;
for(int i = 2 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++)
a[i][j] = a[i - 1][j - 1] + a[i - 1][j] + a[i - 1][j + 1];
for(int i = 1 ; i <= n ; i++)
sum += a[n][i];
cout << sum;
}